Post

[선형대수학] 행렬식(Determinant)

Posted
By Ennik 14 min read

행렬식(결정자, Determinant)

  • 행렬식(Determinant)은 선형대수학에서 중요한 개념으로, 정사각 행렬(square matrix)에 할당된 특정한 스칼라 값이다.
  • 행렬식은 보통 ‘$det$’ 또는 기호 ‘$|$’로 표시된다.

행렬식의 의미

  • 선형변환의 척도(Scale of Linear Transformation) : 행렬식은 행렬이 나타내는 선형변환에 의해 공간이 확대 또는 축소되는 정도를 나타낸다. 예를 들어, 2차원 공간에서 2x2 행렬의 행렬식은 선형 변환에 의해 변형된 면적의 배율을 나타낸다.

  • 역행렬의 존재 여부(Invertibility) : 행렬식의 값이 0이 아니면, 해당 행렬은 역행렬을 가진다.(비특이 또는 가역). 반면, 행렬식이 0이면, 해당 행렬은 역행렬이 존재하지 않는다(특이 또는 비가역).

  • 선형독립의 척도(Linear Independence) : 행렬의 열(또는 행)이 선형독립인지 여부도 행렬식으로 판단할 수 있다. 행렬식이 0이 아니면 열들은 선형독립이며, 행렬식이 0이면 열들은 선형종속이다.

행렬식의 계산

  • 예시로, 2x2 행렬 $A$의 행렬식은 다음과 같이 계산된다:

    \[A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\] \[\det(A) = ad - bc\]
  • 큰 정사각 행렬의 경우, 계산은 더 복잡해지며, 일반적으로 소행렬식(minors)과 공인수(cofactors)를 사용한 전개 또는 라플라스 확장으로 수행된다.

  • 정방행렬 $A\in \mathbb{R}^{n\times n}$의 행렬식(determinant) $|A|$ (또는 $\det A$)는 다음과 같이 계산할 수 있다.

    \[|A| = A_{1,1}\times|A_{\backslash1,\backslash1}| - A_{1,2}\times|A_{\backslash1,\backslash2}| + A_{1,3}\times|A_{\backslash1,\backslash3}| - A_{1,4}\times|A_{\backslash1,\backslash4}| + \cdots ± A_{1,n}\times|A_{\backslash1,\backslash n}|\]

    여기서 $A_{\backslash i,\backslash j}$는 $i$번째 행과 $j$번째 열을 없애버린 행렬이다.

    \[A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 0 \end{bmatrix}\]

    위의 식을 사용하면 아래와 같이 전개된다.

    \[\begin{align*} |A| = 1 \times \left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right | - 2 \times \left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right | + 3 \times \left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right | \end{align*}\]

    이제 위의 $2 \times 2$ 행렬들의 행렬식을 계산하면 된다.

    \[\left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right | = 5 \times 0 - 6 \times 8 = -48\] \[\left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right | = 4 \times 0 - 6 \times 7 = -42\] \[\left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right | = 4 \times 8 - 5 \times 7 = -3\]

    최종결과는 다음과 같다.

    \[|A| = 1 \times (-48) - 2 \times (-42) + 3 \times (-3) = 27\]
  • 행렬식은 선형 시스템, 벡터 공간, 고유값 계산 등 여러 분야에서 중요한 역할을 한다.

  • numpy.linalg 모듈의 det 함수를 사용하여 행렬식을 쉽게 구할 수 있다.

    1
2
3
4
5
6
7
8
9
10

    import numpy as np
import numpy.linalg as LA

A = np.array([
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 0]
    ])
LA.det(A)
#27.0

행렬식의 기하학적 해석

행렬

\[\begin{align*} \begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & a_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_n^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix} \end{align*}\]

이 주어졌을 때, 행 벡터들의 선형조합(단 조합에 쓰이는 계수들은 0에서 1사이)이 나타내는 $\mathbb{R}^n$ 공간 상의 모든 점들의 집합 $S$를 생각해보자. 엄밀하게 나타내자면 \(S = \{v\in \mathbb{R}^n : v=\sum_{i=1}^n \alpha_i a_i ~\mathrm{where}~ 0\leq \alpha_i \leq 1, i=1,\ldots,n\}\)

중요한 사실은 행렬식의 절대값이 이 $S$의 부피(volume)과 일치한다는 것이다!

예를 들어, 행렬

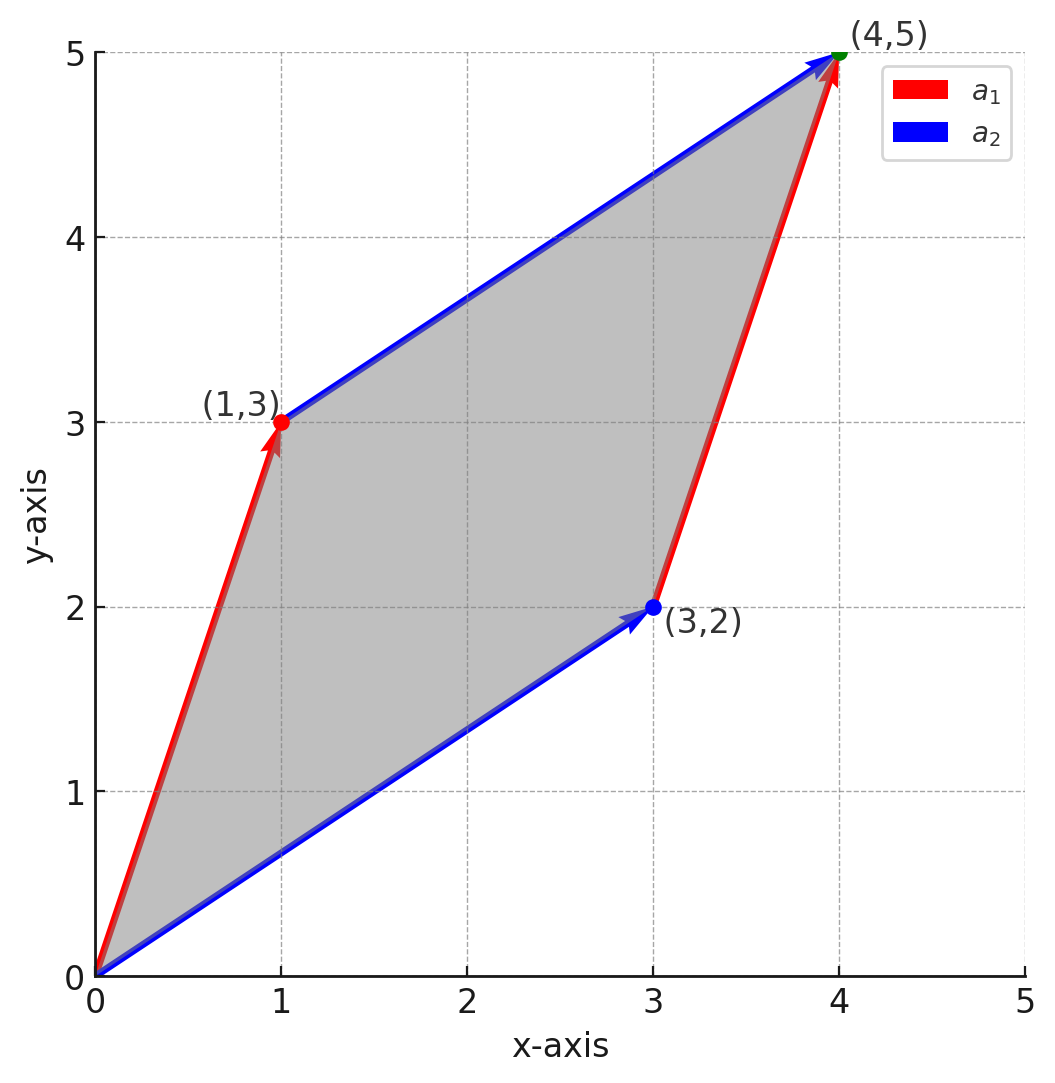
\[A = \begin{bmatrix} 1 & 3 \\ 3 & 2 \end{bmatrix}\]

의 행벡터들은

\[a_1 = \begin{bmatrix} 1\\ 3 \end{bmatrix} a_2 = \begin{bmatrix} 3\\ 2 \end{bmatrix}\]

이다. $S$에 속한 점들을 2차원평면에 나타내면 다음과 같다.

graph

평행사변형 $S$의 넓이는 7인데 이 값은 $A$의 행렬식 $|A| = -7$ 의 절대값과 일치함을 알 수 있다.

행렬식의 성질들

  • $|I|=1$

  • $A$의 하나의 행에 $t\in \mathbb{R}$를 곱하면 행렬식은 $t|A|$

    \[\begin{align*} \left|~\begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & ta_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_n^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix}~\right| = t|A| \end{align*}\]

  • $A$의 두 행들을 교환하면 행렬식은 $-|A|$

    \[\begin{align*} \left|~\begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & a_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_n^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix}~\right| = -|A| \end{align*}\]
  • For $A\in \mathbb{R}^{n\times n}$, $|A| = |A^T|$.
  • For $A, B\in \mathbb{R}^{n\times n}$, $|AB| = |A| |B|$.
  • For $A\in \mathbb{R}^{n\times n}$, $|A|=0$, if and only if $A$ is singular (non-invertible). $A$가 singular이면 행들이 linearly dependent할 것인데, 이 경우 $S$의 형태는 부피가 0인 납작한 판의 형태가 될 것이다.
  • For $A\in \mathbb{R}^{n\times n}$ and $A$ non-singular(역행렬이 존재하는 경우), $|A^{-1}| = 1/|A|$.
  • $|AA^{-1}| = |A||A^{-1}|$

이차형식 (Quadratic Forms)

  • 이차형식은 벡터와 행렬을 사용해 정의된 함수로, 벡터를 정방행렬에 의해 다른 벡터로 매핑하고, 그 결과를 원래 벡터와 내적하여 스칼라 값을 생성한다.
    • 벡터와 행렬의 곱: 먼저, 주어진 벡터를 특정 행렬로 곱한다. 예를 들어 벡터 $x$와 행렬 $A$가 있을 때, $Ax$라는 새로운 벡터를 만든다.
    • 결과 벡터와 원래 벡터의 내적: 변환된 새로운 벡터 $Ax$와 원래의 벡터 $x$의 내적(점곱)을 구한다. 내적은 두 벡터의 각 성분을 곱한 후, 그 결과를 모두 더하는 계산이다.
    • 스칼라 값: 이 내적의 결과는 숫자 하나(스칼라 값)가 된다. 이 값은 원래 벡터와 행렬이 어떻게 상호 작용하는지에 대한 정보를 준다.
  • 벡터의 각 성분과 행렬의 각 요소 간의 관계를 나타내며, 주로 벡터 공간에서의 거리, 각도, 곡률 등을 계산하는 데 사용된다.

이차형식의 전개

  • 정방행렬 $A\in \mathbb{R}^{n\times n}$와 벡터 $x\in \mathbb{R}^n$가 주어졌을 때, scalar값 $x^TAx$를 이차형식(quadratic form)이라고 부른다. 다음과 같이 표현할 수 있다.
\[x^TAx = x^T(Ax) = \sum_{i=1}^n x_i(Ax)_i = \sum_{i=1}^n x_i \left(\sum_{j=1}^n A_{ij}x_j\right) = \sum_{i=1}^n\sum_{j=1}^n A_{ij}x_ix_j\]

아래 전개를 사용하였다.

\[\begin{align*} Ax &= \begin{bmatrix} \vert & \vert & & \vert\\ a_1 & a_2 & \cdots & a_n\\ \vert & \vert & & \vert \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix}\\ &= x_1 a_1 + x_2 a_2 + \cdots\\ (Ax)_i &= (x_1 a_1)_i + (x_2 a_2)_i + \cdots\\ &= x_1 A_{i1} + x_2 A_{i2} + \cdots \end{align*}\]
  • 이 식에서 $A_{ij}$는 행렬 $A$의 (i,j) 번째 요소, $x_i$와 $x_j$는 벡터 $x$의 i번째와 j번째 요소이다. 이차형식은 벡터 $x$의 각 요소가 행렬 $A$를 통해 어떻게 상호작용하는지를 나타내는데, 이는 기하학적으로 또는 물리적으로 여러 상황을 모델링하는데 사용된다.
  • 다음이 성립함을 알 수 있다.
\[x^TAx = (x^TAx)^T = x^TA^Tx = x^T\left(\frac{1}{2}A + \frac{1}{2}A^T\right)x\]

대칭행렬과 이차형식

  • 이차형식에 나타나는 행렬을 대칭행렬로 가정하는 경우가 많다. $x^TAx$는 그 자체로 스칼라 값이고, 전치(transpose)를 취해도 값이 바뀌지 않기 때문이다. 즉, $x^TAx$는 항상 $x^TA^Tx$와 같다. 대칭행렬은 $A = A^T$를 만족하므로, 이차형식을 계산할 때 편리하다.

이차형식의 분류

  • 양의 정부호(positive definite)
    • 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \gt 0$을 만족할 때
    • $A\succ 0$(또는 단순히 $A \gt 0$)로 표시한다.
    • 모든 양의 정부호 행렬들의 집합을 $\mathbb{S}_{++}^n$으로 표시한다.
  • 양의 준정부호(positive semi-definite)
    • 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \ge 0$을 만족할 때
    • $A\succeq 0$(또는 단순히 $A \ge 0$)로 표시한다.
    • 모든 양의 준정부호 행렬들의 집합을 $\mathbb{S}_{+}^n$으로 표시한다.
  • 음의 정부호(negative definite)
    • 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \lt 0$을 만족할 때
    • $A\prec 0$(또는 단순히 $A \lt 0$)로 표시한다.
  • 음의 준정부호(negative semi-definite)
    • 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \leq 0$을 만족할 때
    • $A\preceq 0$(또는 단순히 $A \leq 0$)로 표시한다.

  • 부정부호(indefinite)

    • 대칭행렬 $A\in \mathbb{S}^n$가 양의 준정부호 또는 음의 준정부호도 아닌 경우
    • $x_1^TAx_1 > 0, x_2^TAx_2 < 0$을 만족하는 $x_1, x_2\in \mathbb{R}^n$이 존재한다는 것을 의미한다.
  • Positive definite 그리고 negative definite 행렬은 full rank(행렬의 모든 열 또는 행이 선형독립)이며 따라서 invertible(역행렬이 존재)이다.

Gram matrix

  • 덴마크 수학자 요한 페더센 그램(Jørgen Pedersen Gram)의 이름을 딴 행렬이다.
  • 임의의 행렬 $A$의 열 벡터들 사이의 내적을 요소로 하는 행렬이다.
  • 임의의 행렬 $A\in \mathbb{R}^{m\times n}$이 주어졌을 때 행렬 $G = A^TA$를 Gram matrix라고 한다.
  • 열 벡터들의 내적을 기반으로 하기 때문에, 해당 벡터들의 길이와 사이각에 대한 정보를 포함한다.

Gram 행렬의 성질

  • Gram 행렬은 대칭 행렬이다. 즉 $ G = G^T $.
  • Gram 행렬은 언제나 positive semi-definite이다. 모든 벡터 $x$에 대해 $x^TGx \ge 0$이 성립한다.
  • 만약 원래의 행렬 $A$가 full rank(행렬의 모든 열 또는 행이 선형독립)를 가지며, $m \ge n$이라면 $G$는 positive definite이다. 모든 0이 아닌 벡터 $x$에 대해 $x^TGx > 0$이 성립한다.

기하학적 해석

  • Gram 행렬의 요소는 원래 행렬 $A$의 열 벡터들 사이의 내적을 나타낸다.
  • Gram 행렬의 결정자(행렬식, determinant)는 $A$의 열 벡터들이 형성하는 볼륨(예를 들어, 평행육면체의 부피)을 제곱한 값과 동일하다.
  • 만약 Gram 행렬의 결정자가 0이 아니라면, $A$의 열 벡터들은 선형독립이다.
7.1 선형대수학
Linear Algebra ML Numpy
This post is licensed under CC BY 4.0 by the author.