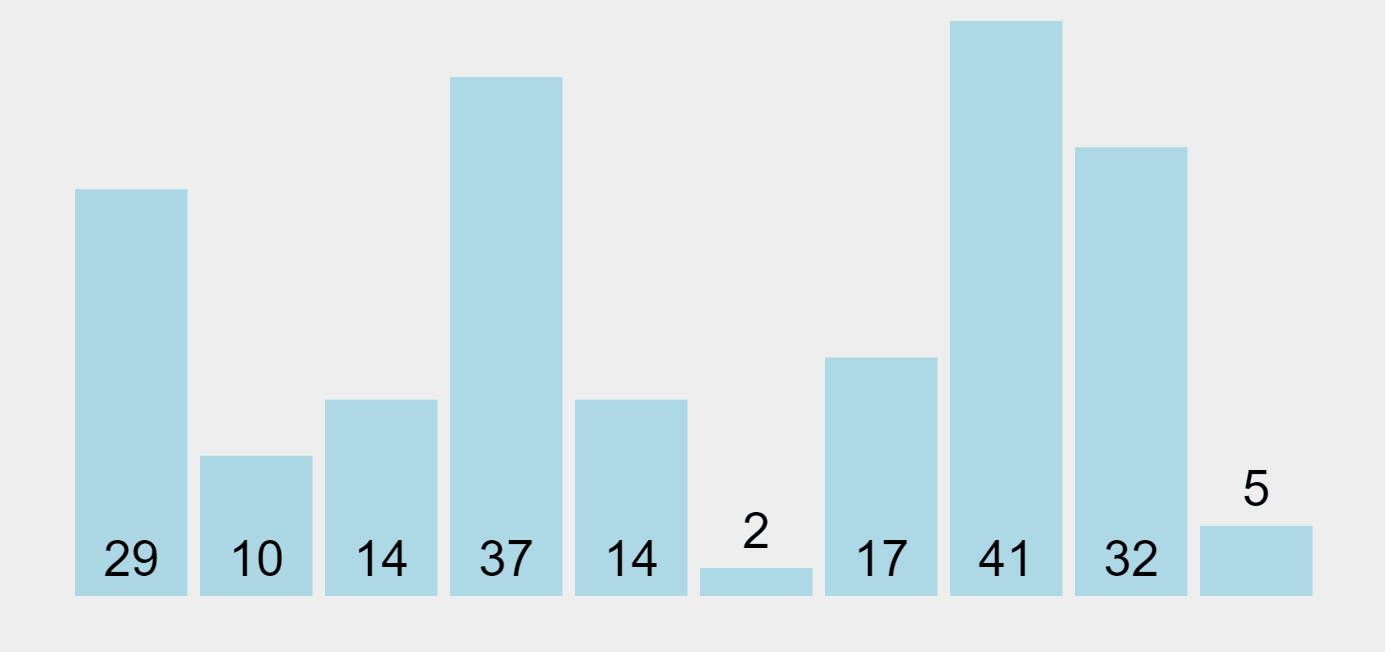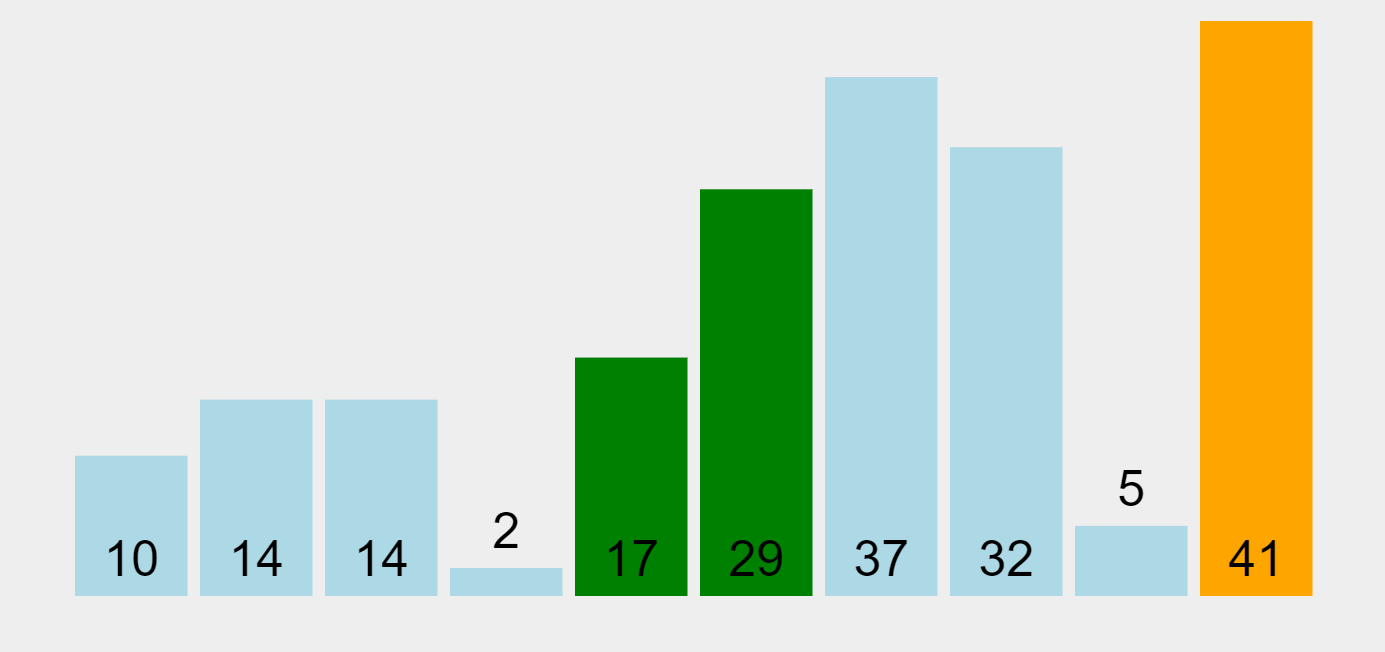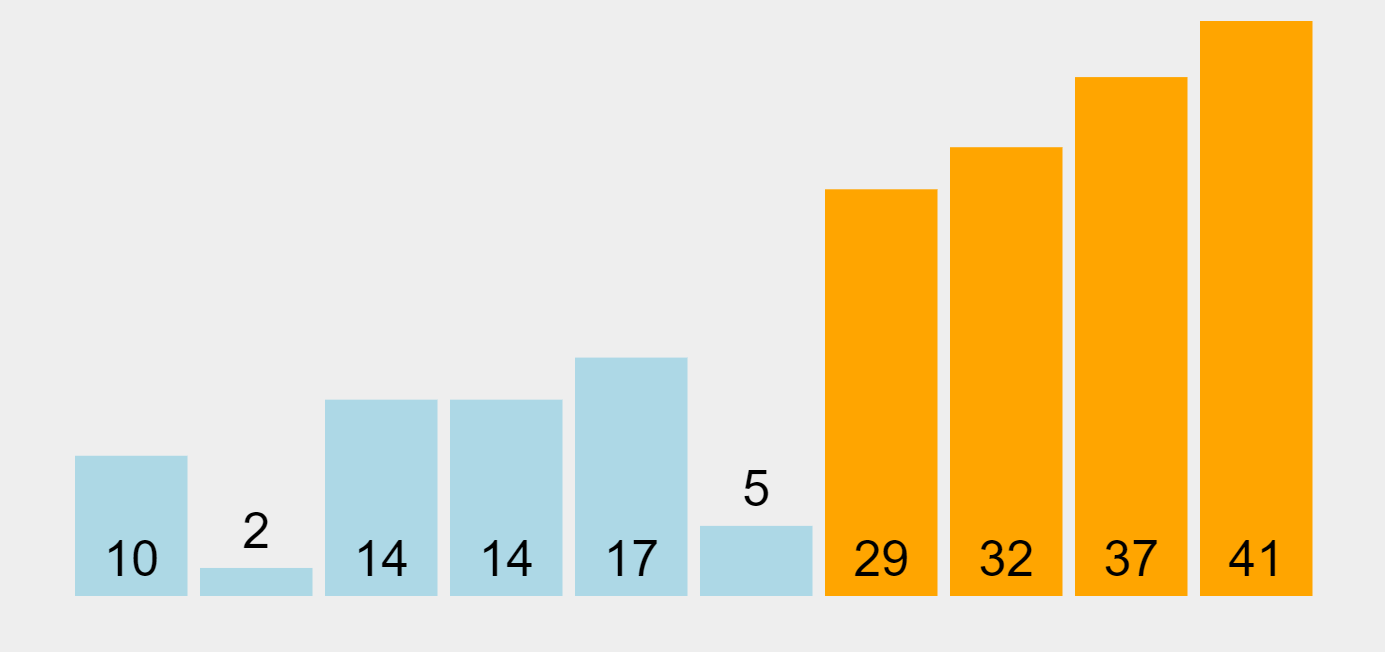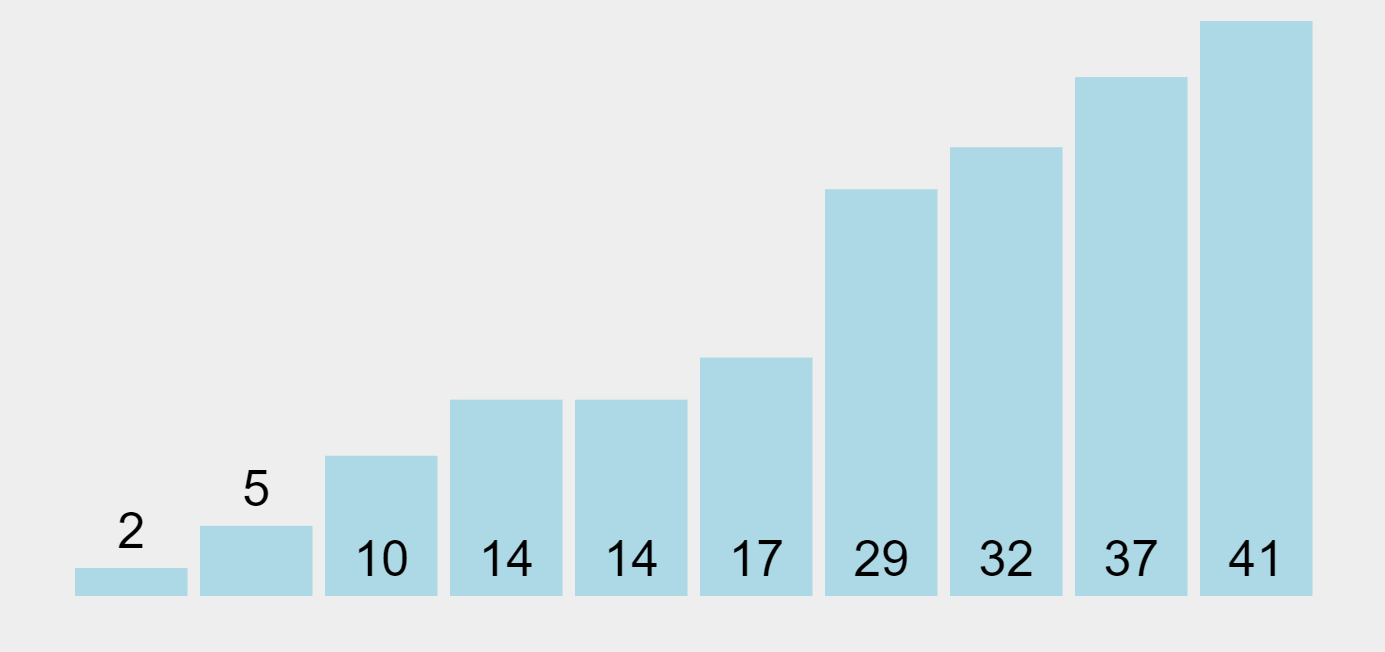[알고리즘] 버블 정렬(Bubble Sort)

버블 정렬

거품이 유리잔 바닥에서 올라오는 것처럼 정렬 과정에서 큰 값이나 작은 값이 배열을 통해 거품(Bubble)처럼 상승하거나 이동한다고 해서 버블 정렬이다.

간단하지만 비효율적인 알고리즘이라 실제로 많이 쓰이지는 알고리즘인데 코딩테스트에서 이 알고리즘을 쓴다면 높은 확률로 시간초과가 나올 것이다. 보통 알고리즘을 공부하지 않고 문제를 냅다 푼다면 자연스럽게 이 알고리즘을 쓰는 경우가 많은 것 같은데 그게 뭔지 알고는 있는 차원에서도 공부할 가치가 있는 알고리즘이다.

이 알고리즘은 배열을 반복적으로 훑으면서 인접한 원소들을 비교하고, 순서가 잘못되어 있으면 교환한다. 기본적인 원리는 작은 값(또는 큰 값)이 버블처럼 배열의 한쪽 끝에서 다른 쪽 끝으로 올라가는 것이다.

버블 정렬의 작동 방식

• 배열의 각 원소를 순회하면서 인접한 원소끼리 비교
• 인접한 원소의 순서가 잘못되어 있으면(예: 오름차순 정렬에서 왼쪽이 오른쪽보다 큰 경우), 이 두 원소의 위치를 바꿈
• 배열의 끝까지 이 과정을 반복
• 배열의 모든 원소가 정렬될 때까지 위의 과정을 전체 배열에 대해 반복

예시: 오름차순 정렬

1. 첫 번째 패스(Pass): 배열을 처음부터 끝까지 순회하면서 인접한 원소를 비교하고 이 과정에서 가장 큰 원소는 계속해서 교환되어 배열의 맨 오른쪽으로 이동한다. 첫 번째 패스가 끝나면 가장 큰 원소가 배열의 맨 오른쪽에 위치.
2. 두 번째 패스: 맨 오른쪽 원소는 이미 정렬된 상태이므로, 그 왼쪽의 원소들만을 대상으로 동일한 과정을 반복한다. 이 과정에서 두 번째로 큰 원소가 끝에서 두 번째 위치로 이동한다.
3. 계속된 패스: 이러한 과정을 배열에 정렬할 원소가 남아있지 않을 때까지 반복한다. 각 패스마다 다음으로 큰 원소가 정렬되어, 오른쪽부터 순서대로 정렬이 완료된다.

예: [4, 2, 6, 3, 9]

만약에 원래 배열이 [4, 2, 6, 3, 9]라면, 첫번째 pass는 다음과 같다.

1. 4와 2 비교: 4가 2보다 크기 때문에 둘의 위치를 바꾼다. [2, 4, 6, 3, 9]

2. 4와 6 비교: 6이 4보다 크고 알아서 잘 배열 되어 있으므로 그냥 넘어간다. [2, 4, 6, 3, 9]

3. 6과 3 비교: 3은 6보다 작으므로 둘의 위치를 바꾼다. [2, 4, 3, 6, 9]

4. 6과 9 비교: 알아서 잘 배열되어 있으므로 그대로 둔다. [2, 4, 3, 6, 9]

→ 이러면 한번의 순회가 끝나는데 이 경우 가장 마지막의 원소가 가장 큰 숫자임이 보장된다. 따라서 다음 순회부터는 가장 마지막의 원소를 제외하고 [2, 4, 3, 6]만 가지고 정렬을 반복한다.

두 원소만 남을 때까지 비교 후 정렬하는 순회를 반복하면 정렬이 모두 완료되고, 이러한 정렬은

[4, 2, 6, 3, 9] → [2, 4, 3, 6, 9] → [2, 3, 4, 6, 9] → [2, 3, 4, 6, 9] →[2, 3, 4, 6, 9]

이렇게 완료된다.

pass의 수

정렬이 완료될 때까지 이루어지는 pass의 수는 어떤 원소가 앞으로 이동하는 가장 먼 거리 + 1이다.

한 pass에서 한 원소가 왼쪽으로 이동할 수 있는 최대 거리가 한칸이기 때문이고

-1이 되는 것은 정렬이 완료되었는지 확인하는 한 번의 pass가 필요하기 때문이다.

파이썬 코드로 나타내면 다음과 같다.

arr = [4, 2, 6, 3, 9]
n = len(arr)

for i in range(n):
    sorted = True
    for j in range(1, n - i): # 오른쪽 끝에서 i개의 원소를 제외하고 반복
        if arr[j - 1] > arr[j]:
            arr[j - 1], arr[j] = arr[j], arr[j - 1]
            sorted = False
    if sorted:
        break

• 내부 루프에서는 range(1, n - i)를 사용하여 이미 정렬된 오른쪽 부분을 건너뛴다.
• sorted 플래그는 한 패스에서 어떤 교환도 일어나지 않았는지를 체크하는데, 만약 한 패스를 완료하고 나서도 sorted가 True라면, 이는 배열이 이미 정렬되었음을 의미하고, 더 이상의 비교는 필요하지 않으므로 루프를 종료한다.

시간복잡도

• 원소가 n개일 때 처음에는 n - 1번 비교하고 그 다음에 n - 2번 비교, n - 3번, … , 1번 비교하고 반복되는 과정의 수가 n - 1이므로 n(n − 1)/2번의 비교가 수행된다.
• 버블 정렬의 시간복잡도는 O(n²)로 상당히 높다.

백준

• 1377, 1517, 1838, 2750, 5531, 11920, 20190, 22877, 23968, 23969,23970, 24046, 24047, 24048, 30010

참고 자료

• 본문 참고
• gif 출처